Supplement B: "Theory of an Ion Wind Device"
(Return to Index Page)

By Robert Seaman
Capt. USAF

Main Document | Supplement A | Supplement B

Copyrighted © by The Townsend Brown family. All rights reserved.



20 January 1960

Whitehall-Rand, Inc.
1019 Dupont Circle Bldg.
Washington 6, D.C.

Dear Sirs,

Thank you for the material you sent two weeks ago, and for the pleasant visit I had with you.

Electrohydrodynamics and the Tri-arcuate Ballistic Electrode have proven to be a very interesting and absorbing subject for my thesis. Enclosed is a copy of a report of my studies so far, that might interest you. The purpose of the report is to stimulate interest in the project, and to set down my thoughts. It is very sketchy, but perhaps something to base future studies on.

I would appreciate any further information you care to send me concerning this work.

Sincerely,

/S/

Robert Seaman
Capt. USAF

CONTENTS

I. Introduction

II. Device Description

Tri-arcuate Ballistic Electrode
Figure 1
Related Information

III. Equations

Velocity and Thrust
Sample Calculations

IV. Experimental Data

Voltage Dependency
Pressure Dependency
Figure 2

V. Need for Data

VI. Summary

Bibliography

II. Device Description:

The following description is of an invention by Whitehall-Rad, Inc. called Tri-arcuate Ballistic Electrode. Information is taken from the company's patent application, personal correspondence, and a personal visit to the company.

First, the invention will be described, and then related information from other applications will be discussed.

TRI-ARCUATE BALLISTIC ELECTRODE

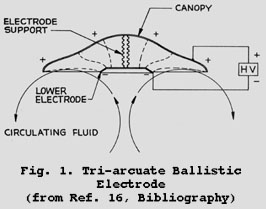Fig.1. Tri-arcuate Ballistic Electrode - (from Ref. 16, Bibliography)

ION WIND DEVICE

I. Introduction

A proposal has been made by Whitehall-Rand, Inc. to use electrostatic fields to ionize an accelerate environmental fluids as a propulsion mechanism. However, no satisfactory theory or description of the forces and velocities produced was submitted. This report is an attempt to fill that need so that prediction of performance, and design improvements may be made. It is not intended that this report will describe all the related phenomena of Ion Wind, nor suggest further use of it.

The theory of the proposed "Ion Wind" device will be presented in the following manner:

First, a description of the mechanism;

Second, the equations for velocities and thrusts will be derived with a sample calculation;

Third, explanations of related phenomena in light of the proposed theory; and

Last, further experimental verification will be suggested.

The above drawing (Fig. 1) represents a device for use in air as the medium, and is about 18 inches in diameter. The upper electrode (canopy) and lower electrode are made of any conducting material, such as aluminum, and are separated by an insulator support.

The electrodes are connected to a high voltage source, of about 150,000 volts for the size of this device. The polarity is selected for maximum voltage difference between the electrodes. Since breakdown voltage in air is highest when the smallest electrode is negative, this is the polarity indicated (Ref. 11: Chapter 13, page 38.)

The flow pattern of the fluid is indicated as a torus. Air molecules and dust particles going near the lower electrode pick up electrons from the corona there, and are accelerated toward the positive canopy. The charged particles collide with the surrounding air, and thus form a wind going to the canopy.

As the circulation passes near, or collides with the canopy, the electrons are released and the neutral (or even positive) air and dust particles are ejected rearward, producing momentum thrust.

Currents carried by the wind are in the one milliamp or less range. This flow pattern is easily seen in a test device by blowing smoke into the flow.

II. Related Information

The flow described above is familiar to the electrostatic precipitation (Catrell) process (Ref. 3, 6, 11, 14, 15). Much work has been done in this area and the sources of ions and their motion in gasses is well known.

Ionization by collision is the main source of charged particles in the process described above. Plus and minus charges are produced in pairs to form a plasma in the corona. The positive ions move toward the negative electrode, and the negative ions toward the positive electrode. Along their path they collide with other neutral particles and exchange electrons, or are themselves again accelerated through a free path in the electric field, only to collide again with neutral particles, until they reach the attracting electrode.

Ion concentrations of 109 ions/cm3 and higher (Ref. 15:71) are typical in corona in air at standard temperatures and pressures. These concentrations can be increased by seeding with easily ionized substances such as Cesium until the medium is close to 100% ionization. One might suppose the charge per ion to be one electronic unit, but this is not the case for dust particles, or other larger than molecular sizes. A particle 100 microns in diameter may be charged with 10 electrons (Ref. 14:1188) to form clusters.

III. Equations

The following theory is derived from the most basic considerations to show the relationships of the factors involved. Very rough order of magnitude calculations may be obtained, but many and various effects are ignored. For more pertinent and precise theories, the reader is referred to References 2, 7, 8 and 13.

Velocity and Thrust

The equation for the velocity of an ion accelerated through a free path is based on the following assumptions:

1. Elastic collisions between particles

2. No forces by ions on neutral molecules

3. The mass of the ions is the same as that of the surrounding medium

4. Homogeneous distribution of ions

5. The energy gained by an ion accelerated over a mean free path is less than the thermal energy of the surrounding molecules

The force on a charged particle in an electric field is give by:

F = qE

where:

F = force (newtons)

q = charge (coulombs)

E = electric field strength (volts per meter)

Therefore, the work done by the field on the particle must equal the kinetic energy gained, or:

Work = Fd = qEd = 1/2mVd2

where:

d = distance through which ion is accelerated (meters)

m = mass of ion (kilograms)

Vd = drift velocity (meters / second)

Where equation (2) is solved for drift velocity,

Vd = (2qEd / m)1/2     (3)

When d is assumed to be the mean free path, L (meters), of a molecule in a gas with thermal energy 1/2 mc2 (c = thermal velocity), then equation (3) can be written (Ref. 2:35)

Vd = qE / mc     (4)

This is the velocity of the ion wind under the listed assumptions. When the energy gained by the ions is greater than the thermal energy of the medium, equation (3) becomes (Ref. 8:70)

Vd = (1.147qEd / m)1/2     (5)

where d is now a function of (E / p)1/2 where p is the gas pressure. It is clear that equation (3) is a good approximation.

The momentum thrust of this device is given by the traditional rocket equation,

T = m'Ve     (6)

where,

T = thrust (newtons)

m' = mass rate of flow (kilograms / second)

Ve = exhaust velocity (meters / second)

Sample Calculations

The following example is representative for atmospheric air. From equation (4), and typical values for the parameters from the references, the Ion Wind velocity can be computed. Let:

E = 107volt / m     (Re. 9:116)

L / c = 10-9 sec.     (Ref. 8:41)

q = e- = 10-19 coul.     (Ref. 15:71)

m = 10-26 kg.     (Ref. 4)

Equation (4) then becomes:

Vd = qEL / mc = (10-19 coul.)(107 volt)(10-9 sec.) / 10-26 kg m

Vd = 105 m / sec

By momentum exchange the ions drive the air with a wind velocity given by the equation for conservation of momentum:

PaVa = PiVd     (7)

where,

Pa = density of air

Va = wind velocity of the air

Pi = density of ions.

Assuming the concentration of ions is 1013 ions / cm3 in air with 1019 particles / cm3, and assuming their masses are equal, equation (7) yields:

Va = (Pi / Pa) Vd = (1013 / 1019) 105 m / sec = 0.1 m / sec

This value is similar to wind velocities of one foot per second, as found in the references (Ref. 15:72, and 11:chap 13, p 39).

The current density would be given by:

j = m'i q     (8)

where m' is the ion flow per unit area. Using values found above,

j = (1013 ions / cm3) (10 cm / sec) (10-19 coul / ion) = .01 ma / cm2

The thrust is given by equation (6), if it is assumed the exhaust velocity is equal to the wind velocity calculated above. This also assumes the velocity is directed opposite to the direction of motion. The density of atmospheric air is:

.00238 slug / ft3, so that equation (6) yields:

T = m'aVe = (.00238 slug / ft3) (1 ft2 / sec2)

T = .00238 lb / ft2

The results of these calculations agree with those values observed by Whitehall-Rand, Inc.

It should be emphasized that many factors have been ignored. Some of these are:

1. Temperature changes
2. The clustering effect of dust particles
3. Non-uniform field
4. Inhomogeniety

IV. Experimental Data

Many characteristics of the Tri-arcuate devices were recorded by Whitehall-Rand, Inc., after extensive experimentation in air, and transformer oil. Most of these are easily explained in light of the above theory.

Voltage Dependency

It was experimentally determined that the thrust was proportional to the voltage squared. This characteristic is probably a consequence of space charge limitation (Ref. 15:68). Rewriting equation (6) by substituting:

m'a = PaVa = PiVd

T = PaVa2 = PiVaVd     (9)

But by equation (8):    PiVa = m'i = i / q, thus:     (10)

T = (i / q) Vd     (11)

In the case of space charge limitation, the current density j is given by the Langmuir-Child Law as:

j = k1 E3/2 / d1/2     (12)

where k1 = a constant. Substituting the value for j from equation (12), and Vd from equation (3), equation (11) becomes:

T = (k2 / m) E2     (13)

where k2 is a second constant. Equation (13) illustrates the dependence of the thrust on the square of the field intensity.

Pressure Dependency

The following were drawn from data obtained by Whitehall-Rand, Inc.:

The upper curve shows the thrust constant with pressure, and the lower curve shows the decrease in current i with pressure. These data were taken at constant voltage. The break in the curves in the neighborhood of 10-3 mm Hg is the result of the gas breakdown. (Ref. 9) Sparking was observed, with the resulting increase of current, and power source cut off. As the pressure was further decreased, breakdown voltage increased again, as predicted by theory, until no sparking was observed. At this point measurements were resumed.

The thrust curve is seen to be a straight line of constant value. This is predicted by equation (13) under the space charge limitation. And, the current curve decreases with pressure as predicted by equation (12) since d, the distance between collisions, increases as the pressure decreases.

Other characteristics reported by Whitehall-Rand are explainable by the above theory.

V. Need for Data

Further experimentation is needed to verify the theory suggested above to explain the thrust from the Ion Wind produced in the Tri-arcuate Ballistic Electrode. The following list suggests some possible phases:

1. Examination and plotting of the electric field around and in the device,

2. Measurements of the ion flow and velocity and the air flow and velocity,

3. Measurement of the charge and mass of the ions,

4. Further measurement of the pressure and voltage relationships at low pressures,

5. Determination of optimum size and shape relations related to drag,

6. Determination of the constants in the space charge limited current and thrust equations,

7. Application to the space environment, and limitations of the theory.

VI. Summary

This report has attempted to present a theory to support the data reported by Whitehall-Rand, Inc., in connection with their invention The Tri-arcuate Ballistic Electrode. Thrust can be obtained through Ion Wind, given by the space charge limited equation

T = (k2 / m) E2     (13)

Verification of this theory is necessary, and further data is needed on the characteristics of this device.

Bibliography

1. Alfven, Hannes. Cosmical Electrodynamics. Oxford:; Clarendon Press, 1950.

2. Cobine, J.D. Gaseous Conductors. New York: McGraw-Hill Book Co, Inc., 1949.

3. Deutsch, W. "Is the Action of Electrical Gas Purification Due to 'Electrical Wind'?" Annals der Physik (Fifth Series), 9:249-264, (1931).

4. Hausmann, Erich, and E.P. Slack. Physics (Third Edition). New York: D. Van Nostrand Co., Inc., 1948.

5. Jeans, Sir James. The Mathematical Theory of Electricity and Magnetism (Fifth Edition). Cambridge: Cambridge University Press, 1946.

6. Lapple, C.E. "Dust and Mist Collection," in Chemical Engineering Handbook (Third Edition), edited by J.H. Perry. New York: McGraw-Hill Book CO, Inc., 1950, p. 1039.

7. Llewllyn-Jones, Frank. Ionization and Breakdown in Gases. New York: John Wiley and Sons, Inc., 1957.

8. Loeb, L.B. Basic Processes of Gaseous Electronics. Berkeley: University of California Press, 1955.

9. --------. The Mechanism of the Electric Spark. Stanford University: Stanford University Press, 1941.

10. --------. "Recent Developments in Analysis of Positive and Negative Coronas in Air," Journal of Applied Physics, 19:882-896, (October, 1948).

11. Magill, P.L. et al ed. Air Pollution Handbook. New York: McGraw-Hill Book CO, Inc., 1956.

12. Perel', V.I. "Calculations of the Drift Velocity of Ions in the Electric Field in Their Gas." Soviet Physics JETP, 5, No. 3:440-444, (October, 1957).

13. Thomson, J.J. and G.P. Thomson. Conduction of Electricity Through Gases (Third Edition). England: Cambridge University Press, 1928, Vol. I and II.

14. White, H.J. "Particle Charging in Electrostatic Precipitation." Transactions of American Institute of Electrical Engineers, 70(Pt II):1186-1191, (1951)

15. --------. "Role of Corona Discharge in Electrical Precipitation Processes." Electrcial Engineering, 71:67-73, (1951).

16. Whitehall-Rand, Inc. Patent Application for Tri-arcuate Ballistic Electrode. 1959.



Please be advised that this document is copyrighted © by The Townsend Brown family. All rights reserved. Please see Legal and Copyright Information for additional copyright information.